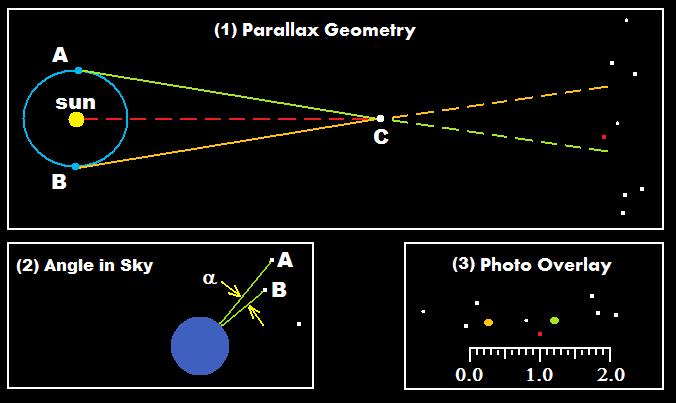
Cosmic Distance Ladder

Cosmic distances are determined by a number of methods. Many of these methods depend on distances determined from other methods. By determining the distances to nearby stars, and learning the nature of the various celestial bodies, allows us to calculate the distance to more remote objects. Here is an overview of some of the tools used by astronomers to determine distance.

Parallax.

This is the basic use of triangulation. This is the method that surveyors use to determine the distance to a landmark. A surveyor will measure the angle between three points of a triangle, two of the points are measuring locations, the third is the target in question.

The same methodology is used to calculate distance to nearby stars. Only rather than measuring the angle from different places on Earth, the measurement is done from different times of the year, taking advantage of the Earth's orbit.

The real distance between two stars is not directly measured but the angle between them is. (see figure 2 below) This can be done by locating one star in the cross hairs of a telescope, then slewing the telescope by a measured angle until the other star is now centered on the cross hairs. The angle rotated is the angle between those stars in the sky. Photos taken at a given magnification will have a coresponding scale for the angle per unit length in a the photo.

When photos are overlaid from different times of the year, very distant stars will not change position with respect to the Earth's movement in its orbit, but the nearby stars will. By measuring the angle between a near star and a distant star, at different times of the year, the distance is found by:

d=D/beta
where D is the diameter of the Earth's orbit, and beta is the maximum change in the star's angular position over a year, in radians (1 radian=57.3°). The distance is then in the same units as those used for D.

This formula reduces to:

d=1/beta
when beta is given in arcseconds, giving the distance in parsecs (1 parsec = 3.26 light years). [ref112, pg368]

In figure 1, points A and B represent different times when photos were taken. In each photo, star C appears in a different location relative to the red star in the background. When the photos are overlaid in figure 3, its angular position change can be measured. (The position from A is shown in green, the position from B is in orange.) Typically, the angle will be less than one arcsecond. A tenth of an arcsec change would indicate a distance of 10 parsecs.

Standard Candles

Once the distance to nearby objects were determined, their luminosity could be calculated. The luminosity is the amount of light energy that the source object is producing. Since the brightness we measure from Earth (or the flux density of the light) is reduced because of the spreading of light acording to the following formula:

F=L/4πr², where F is the measured flux density (light energy recieved per unit of area), L is the luminosity of the source, r is the distance.

If you know the luminosity of the source object and can measure its flux density reaching Earth, then you can calculate its distance by solving the above formula for the distance (r):

r=squareroot(L/4πF)

This is where standard candles come in. Certain types of stars have known luminosity. You can easily measure the flux density here and then calculate the distance.

For more distant objects, such as distant galaxies, supernovae can be used as standard candles. Specifically, type Ia supernovae, because this type of supernova has a known light curve and peak luminosity.

Doppler Effect

The velocity toward or away from Earth can be determined by the doppler shift of the frequency of the light emitted from the distant object. This is the same effect that is observed when a passing train blows its horn. As the train approaches its frequency is shifted higher, due to the successive wave crests being closer together than if it were at rest. Once the train passes, the effect is reversed as the train is now moving away. Now the wave crests are farther apart as the each wave is emitted from farther away, and the observer notices a downward shift in the frequency of the horn.

Like sound waves, light is also doppler shifted by relative motion. Since many light sources have known frequencies, we can calculate the relative motion from the difference with the frequency we measure on Earth. It is from this method it has been determined that all distant galaxies are moving away from us.

Hubble's Law

Being able to measure both distance and relative velocity revealed that all distant galaxies are moving away from us in proportion to their distance. This is related by Hubble's law, d=V/H, where V is the relative velocity, H is Hubble's constant (about 72 km/s/MPc), and d is the distance. So to find the aproximate distance to a far away galaxy, one only needs to use the Doppler shift of the frequency to determine the relative velocity, then use Hubble's law to calculate the distance. If velocity is entered in km/s then the distance calculated is in megaparsecs (MPc). One megaparsec = 1,000,000 parsecs = 3,260,000 light years = 9.47 trillion km. This large unit of measure is convenient due to the massive distances between galaxies.

Return to General Science

Support Us: by liking us on Facebook or sharing our site with a friend. See the following links:

Visit us on Facebook

Share as Bookmark, Tweet, message, etc.

updated Oct 15, 2012
(c) 2012 RareUniverse.Org
(see our terms of service)